The Power of Compound Interest
Albert Einstein called compound interest "the eighth wonder of the world. He who understands it, earns it ... he who doesn't ... pays it."
If an idea is powerful enough to inspire that level of awe from Einstein, I'm secure enough to admit my consistent and ceaseless wonder at it.
Ben Carlson has a fantastic blog post on turning the power of compound interest into numbers that resonate. Rather than summarize it here, I highly recommend clicking the link.
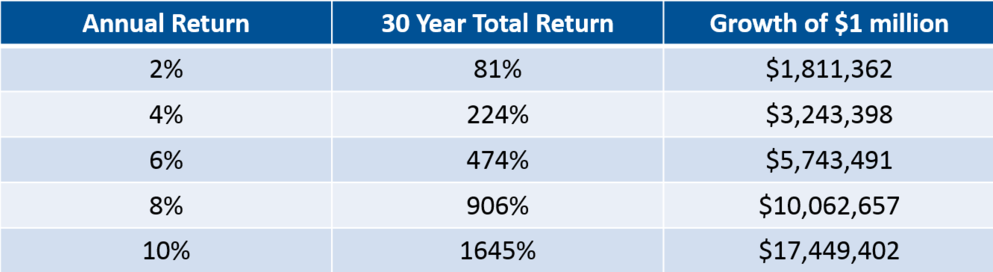
The above chart is taken from Carlson's blog and reproduced with a third column translating total return to dollars.
Here is where investing and financial planning dovetail. When we do retirement planning for clients, our investment returns assumptions have a DRAMATIC effect on the viability of retirement spending assumptions. As seen above, a 2% lower return to a couple in their 30s will mean a halving of their retirement bucket. That may mean tens of thousands of dollars less in annual retirement spending.
Longer projected lifespans mean that we need to plan for retirements of 30 or more years. Having more money saved for retirement isn't a matter of having better vacations, it may be a matter of not having to worry about running out of money. Moreover, what retirees earn on their investments during retirement will have a similar impact on the health of their retirement spending.
The above illustrates how vital it is for people to properly allocate their retirement savings plans (i.e. your 401(k)). Too many have sub-optimal retirement allocations and miss out on the awesome power of compound interest. It's a multi-million dollar mistake mindlessly made when filling out a 401(k) enrollment form. Guidance by an expert can make a gigantic difference.
Example of the Power of Compound Interest
Recently, we looked at some portfolios' historical returns. On their faces, the differences in annualized return didn't seem dramatic. One portfolio had outperformed another with modestly less equities and more bonds by 0.24% annualized (7.17% to 6.93%) over 25 years. An aggressive portfolio of all equities had outperformed a conservative portfolio of mostly bonds by 0.85% (7.54% to 6.69%) over 25 years. Seemingly, hardly enough of a difference to make it worth taking extra risk, right?
Well, if you had invested $1 million in each portfolio, after 25 years that extra 0.24% would have translated into $301,516 more ($5,461,509 to $5,159,993). The extra 0.85% would have meant an extra $1,085,088 ($5,959,468 to $4,874,380). Wow.
These numbers dwarf my expectations using (too) simple math. My first reaction was to estimate using straightforward multiplication:
$1 million x 0.24% = $2400 x 25 years = $60,000
$1 million x 0.85% = $8500 x 25 years = $212,500
Only off by a factor of 5.
We come across examples like this all of the time. And I'm always impressed. At least I'm in good company.